The Infidel wrote:Both people see the other person's watch ticking more slowly than their own. However, the person that ran away will still age less than the person who stayed still.
OK, this baffles me. I feel like I can toss normal logic out the window.[/quote]
It's actually just basic geometry. Let me make an analogy in the ordinary Euclidean plane first.
Suppose there are two people, A and B, that stand on a plane very close to each other, so they are essentially located at the same point. However, they're facing in different directions, and both decide to draw an
x-axis is to the right and
y-axis to the direction they're facing. So the situation is something like this:
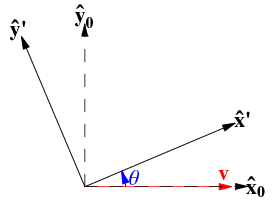
I'm cribbing the diagram from somewhere else. Let's say A's axes are along the x̂₀,ŷ₀ vectors and B's axes are along the x̂,ŷ vectors.
Imagine that both persons absolutely insist on measuring things along those personal axes, calling the length in the
x direction
width and length in the
y-direction
depth.
Code: Select all
^y A and B are stand at O, angle θ.
| Person A places a rod of unit length
y' _-|Q along OQ.
\_- | -> A says the rod is has depth OQ = 1.
P\ |
\ | Person B looks at the same rod, but
\ | measures depth along B's own y-axis.
\| -> P is a right angle
O -> B says the rod's depth is OP=cos θ.
Thus, A thinks B's measurements are just wrong by a factor of cos θ. Now B tries the same thing:
Code: Select all
^y
y' | Person B places a rod of unit length
\______| along OP.
P\ |Q -> A says the rod has depth OP = 1.
\ |
\ | Person A looks at same rod, but
\ | says it has length OQ = cos θ.
\ |
\|
O
What's going on here?
Each person concludes that the
other's measurements of
depth are wrong by the same factor! But there's obviously no real contradiction there; the apparent incongruity is simply because each of them insists on projecting to their personal coordinate axes, so their measurements refer to different things.
If you understand the above scenario, you're in good shape to understand time dilation. Instead of a
y-axis, suppose we have a
t-axis. We're in spacetime, where the history of each object's location at each instant of time traces out a curve, a
wordline. For an inertial observer, that worldline is straight, and so can serve as the usual sort of Cartesian coordinate axis. "Facing in a different direction" is analogous to having a different velocity: if an object's wordline is parallel to some observer's
t-axis, then it's staying on the same place (same
x-coordinate), and in general the slope of some object's worldline, Δx/Δt, is a
velocity.
As before, observers measure
duration as length along their
t-axis, and because they can have non-parallel temporal axes, they each think the other is wrong by exact same factor. The only thing that's really different is that the geometry is pseudo-Euclidean, with angles working a hyperbolically--instead of ordinary cosine (cos), they're related via hyperbolic cosine instead (cosh). The hyperbolic angle between different temporal axes is usually called 'rapidity' in physics, and the hyperbolic cosine of that angle is the Lorentz factor γ.
Magis wrote:This doesn't change the fact that the one who accelerated away will ultimately age more slowly. If I have more time later today I can explain a simplified scenario that shows how the problem is not actually symmetric, and why it is specifically the traveler who ages slowly and not the person who stays still.
We can back up a little bit.
-- In Euclidean geometry, straight lines are have give the
shortest distance between any two points on them.
-- In special relativity, straight worldlines (zero acceleration) give the
longest distance (duration) between any two points (events) on them.
The flip of straight lines from shortest to longest is because of the slightly different geometry (STR's spacetime is pseudo-Euclidean), but those two things are completely analogous. And just like the very intuitive triangle inequality,
-- In Euclidean geometry, if you go from A to C in a straight line, the distance you traverse is shorter than if you make a detour from A to B to C (unless A,B,C collinear).
-- In special relativity, if you go from A to C in a straight line (inertially), the duration you experience is longer than if you make a detour from A to B to C (unless A,B,C collinear).
Vejut wrote:I believe part of it is that the basic coffee-book relativity is special relativity. It deals with constant speed reference frames. Accelerating frames, like somebody slowing down to turn around and come back, or just turning, need the use of general relativity, which I know very little about beyond the fact that even simple stuff for it needs matrix math...
No,
Darth Holbytlan is correct. Special relativity has absolutely no problem dealing with acceleration--it actually would be kind of useless if it couldn't do that.
